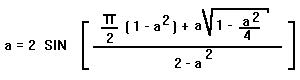Problème de la vache attachée à un piquet planté sur la périphérie d'un champ rond
Ce problème m'a été proposé par un professeur d'ANALYSE à l'ESME SUDRIA, Mr. Rapp, du temps (1985) où j'étais alors étudiant en classe préparatoire. Dans le cadre du calcul des intégrales de fonctions, nous avions à maîtriser divers procédés d'intégration. Le problème de la vache est intéressant, car il nécessite de découper en plusieurs parties le domaine d'intégration. Du choix de cette division découle le succès ou l'échec du calcul.
Enoncé du problème : Calculer la longueur de la corde qui retient une vache attachée à un piquet, pour que celle-ci ne broute que la moitié de l'aire du champ circulaire, sur la périphérie duquel est planté le piquet.
Si la corde est trop courte voici ce qui risque de se produire :
La vache est en phase de décomposition.
Si la corde est trop longue, voici ce qui peut aussi arriver :

La vache grossit d'une manière démesurée, son alimentation est excessive.
L'idéal est alors obtenu lorsque la longueur de la corde, calculée au mieux, permet à la vache de ne brouter que la portion de champ qui lui est attribuée.

Nous observons ici l'évolution d'une vache en parfaite santé.
Pour aborder le problème nous devons adopter un système de représentation bien adapté. C'est le système de coordonnées polaires qui se prête le mieux à la résolution de ce type de problème.
Voici le schéma présentant l'objet de notre calcul :
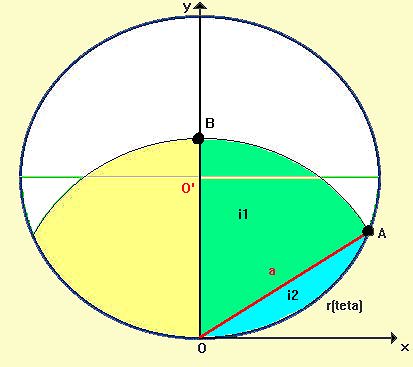
La longueur de la corde que nous désirons calculer est représentée par le segment rouge noté "a".
Le grand cercle noir délimite deux domaines :
Un domaine non coloré.
Un domaine coloré.
Chaque aire de chaque domaine est égale. La valeur de l'aire totale délimité par le cercle est : PI.(R^2).
où R est le rayon du grand cercle. R est égal à la valeur algébrique du segment OO'. Pour simplifier le problème, nous posons : R = 1.
L'aire du cercle vaut donc : PI = 3.141592654....
L'aire de la partie colorée vaut donc : PI / 2.
Pour encore simplifier le problème, on observe une symétrie par rapport à l'axe OY. Donc, il suffit de calculer l'aire de la partie colorée à droite de l'axe OY, puis de multiplier le résultat par 2.
Regardons de plus près la zone contenue entre l'arc de cercle OA, l'arc de cercle AB, et le segment BO.
Nous voyons deux zones :
Une de couleur verte, que nous appelons i1.
Une de couleur bleue que nous appelons i2.
Calcul de I1 :
C'est un calcul assez classique : on utilise la formule de l'intégrale d'un secteur angulaire donc les bornes sont connues.
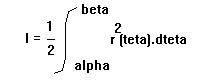
où beta = PI/2 et alpha est égal à l'angle formé entre l'axe OX et le segment OA, on écrit aussi alpha = (OX,OA).
La difficulté consiste à déterminer alpha. Pour cela nous devons écrire l'équation du rayon qui décrit l'aire I2.
Equation du rayon (ro) décrivant l'aire I2 :
En fait, il s'agit de l'écriture en coordonnée polaire, à partir du point O, de l'équation du cercle dont le rayon OO' vaut 1. On a :
ro = 2.SIN(teta), où teta varie entre 0 et PI/2 pour décrire le cercle total, et entre 0 et alpha pour l'arc de cercle OA.
Lorsque teta = alpha, alors ro = OA = a (comme indiqué sur le schéma).
Récapitulons :
Pour teta = alpha alors ro = 2.SIN(alpha) = a. D'où alpha = ARCSIN(a/2)
Nous pouvons alors écrire la valeur de I1 :

D'où I1 = (1/2).a^2.[PI/2 - ARCSIN(a/2)].
Calcul de I2 :
Ici le calcul est également classique; la difficulté réside dans l'écriture du rayon (ro) que nous avons résolue ci-dessus. Donc nous posons directement :

Or COS(2.teta) = 1 - 2.[SIN(teta)]^2,
d'où [SIN(teta)]^2 = (1 - 2.COS(teta)) / 2
Ainsi en réinjectant dans I2 nous obtenons :

A noter que ARCSIN(a/2) n'est possible que si a est inférieur ou égal à 2. Donc les solutions que nous trouverons ultérieurement devront satisfaire cette condition.
Ainsi I2 = ARCSIN(a/2) - (1/2).SIN[2.ARCSIN(a/2)]
Or SIN(2.X) = 2.SIN(X).COS(X)
Donc I2 = ARCSIN(a/2) - (1/2).[2.(a/2).COS(ARCSIN(a/2)] = ARCSIN(a/2) - (a/2).COS[ARCSIN(a/2)]
Nous utilisons les formules du cercle :
Ainsi COS(a/2) = SQRT[1 - [SIN^2(a/2)] ] = SQRT[1 - (a^2 / 4)] (avec SQRT = racine carrée)
D'où I2 = ARCSIN(a/2) - (a/2).SQRT[1 - (a^2 / 4)]
A ce stade du raisonnement nous avons 2 équations :
1) I1 = (1/2).a^2.[PI/2 - ARCSIN(a/2)]
2) I2 = ARCSIN(a/2) - (a/2).SQRT[1 - (a^2 / 4)]
Or nous savons que l'aire broutée par la vache doit être égale à PI/2. Donc :
2(I1 + I2) = PI /2
Après transformation des équations nous trouvons :
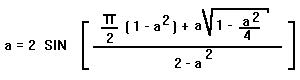
Cette équation n'est pas explicite. C'est ce que l'on appelle une équation implicite. Pour déterminer "a", seul le calcul numérique peut venir en aide. On peut choisir une méthode de dichotomie, ou simplement rentrer l'équation dans une calculatrice évoluée (type HP48G), et utiliser la fonction SOLVE qui rend bien des services.
On trouve alors pour la longueur de la corde retenant la vache :
a = 1.158728472...
Je rappelle que le rayon R du cercle a été choisi égal à 1 pour des raisons de simplifications de calcul. Il va de soi que pour trouver la longueur de la corde d'un cercle de rayon R différent de 1, on multipliera la constante par la valeur du rayon.
a(réel) = R x 1.158728472...
Si des esprits aventureux souhaitent aller plus loin dans l'extraction des décimales de cette constante, ils pourront aller faire un tour sur la page "Calculs en multiprécision" qui sera prochainement disponible.
Quant aux esprits chagrins, qui existent aussi, ils s'élèveront contre ce résultat en invoquant une solution noble, c'est à dire en calcul analytique, et non plus numérique. Je ne sais pas si elle existe. Si c'est le cas, j'aimerais également la connaître.
Enfin, voici aussi la valeur de l'angle teta, ou encore (OX,OA).
teta = ARCSIN(a/2) = 0.6179484615...rad = 35,4058388 °
Questions subsidiaires :
1) Quelle est la race de la vache ? Si vous ne l'avez pas reconnue, je vous recommande d'aller voir l'excellent site dont voici l'adresse :
Toutes les races bovines de la terre
2) Si la vache était anglaise, quelle serait la probabilité pour qu'elle broute la terre à l'extérieur du champ rond ?