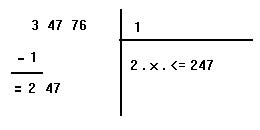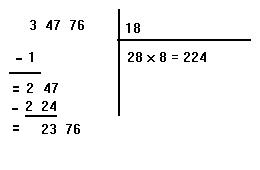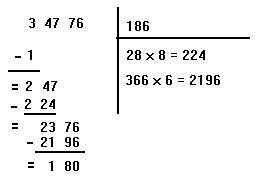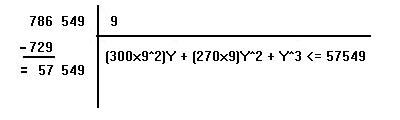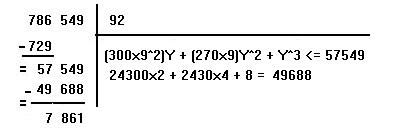Extraction des racines carrées et généralisation de l'algorithme d'Euclide à l'ordre n


I. EXTRACTION DES RACINES CARREES



L'algorithme d'Euclide est le suivant :
Supposons que l'on souhaite extraire la racine carrée de 34776. On pose l'opération comme une division, en plaçant à gauche le nombre dont on veut calculer la racine. On le sépare en tranches de 2 chiffres à partir de la droite. Voici ce que l'on obtient :


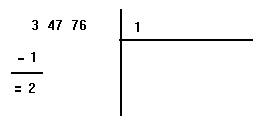
On recherche alors quel chiffre le plus grand élevé au carré est inférieur ou égal à la tranche de gauche (3). On trouve 1, car 2^2 = 4, trop grand. On pose 1 à droite de la barre verticale. On dit : 1 au carré égale 1 que l'on pose sous la tranche de gauche. On soustrait alors ce nombre de la tranche au dessus, et l'on obtient 2.

On "descend" alors la tranche immédiatement à droite de la précédente (47) à coté du nombe 2. On obtient la configuration ci-dessous.


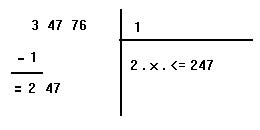
L'astuce consiste alors à mutliplier le nombre en haut à droite par 2, puis à placer sous la barre horizontale le résultat. On obtient 2 x 1 = 2, que l'on écrit sous la barre horizontale. On dit alors : quel chiffre placé à coté de ce 2, et multiplié par lui même donne le plus grand résultat proche de 247 ? On trouve 8. En effet, 28 x 8 = 224, alors que 29 x 9 = 261. Ce résultat (224) est placé sous 247 et l'on effectue la soustraction. On trouve 23. Quant au chiffre 8, il est placé au dessus de la barre horizontale à droite du chiffre 1. On obtient la configuration suivante :



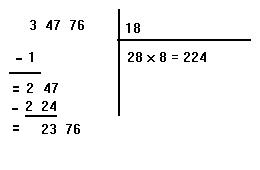
On abaisse alors la tranche suivante (76) et l'on réitère le procédé. On multiplie 18 par 2, on obtient 36. Ce nombre est écrit sous la barre horizontale, puis l'on dit à nouveau : quel plus grand chiffre placé à droite de 36 et multiplié par lui même donne un résultat inférieur ou égale à 2376 ? On trouve 6. En effet, 366 x 6 = 2196 alors que 367 x 7 = 2569 (trop grand). Le nombre 2196 est placé sous 2376, tandis que le chiffre 6 est placé à droite de 18 au dessus de la barre horizontale. La racine carrée de 34776, à l'unité près, est donc 186. Si l'on souhaite continuer le calcul avec les décimales, il suffit de descendre à chaque fois une tranche égale à 00 et de réitérer le processus.




___________________________________________________________

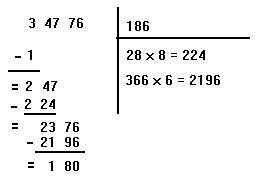
II. EXTRACTION DES RACINES CUBIQUES

La technique va être présentée de la même façon que ci-dessus. La démonstration suit au bas de cette page. Pour l'instant on voit simplement comment calculer par exemple la racine cubique de 786549. On pose l'opération comme une division, en plaçant à gauche le nombre dont on veut calculer la racine. On le sépare en tranches de 3 chiffres à partir de la droite. Voici ce que l'on obtient :


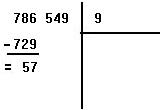
On recherche alors quel chiffre le plus grand élevé au cube est inférieur ou égal à la tranche de gauche (786). On trouve 9, car 9x9x9 = 729 est le maximum que l'on puisse atteindre. Et c'est encore inférieur à 786. On pose 9 à droite de la barre verticale. On dit : 9 au cube égale 729 que l'on pose sous la tranche de gauche. On soustrait alors ce nombre de la tranche au dessus, et l'on obtient 57.

On "descend" alors la tranche immédiatement à droite de la précédente (549) à coté du nombe 57. L'astuce consiste alors à calculer 2 coefficients :
Le premier vaut : le carré du chiffre en haut à droite multiplié par 300. On obtient : 9x9x300 = 24300.
Le deuxième vaut le chiffre en haut à droite multiplié par 30. On obtient 9x30 = 270.
Ces coefficients sont ensuite injectés dans l'inéquation en Y du troisième degré suivante :
(24300.Y) + (270.Y^2) + (Y^3) <= 57549.
L'inconnue de cette équation est Y, un chiffre que l'on doit trouver afin de s'approcher au plus près de 57549 sans le dépasser.


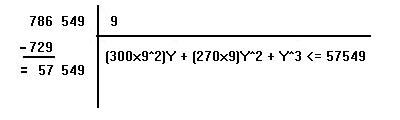
On trouve 2. En effet, (24300x2) + (270x2x2) + 8 = 49688 est inférieur à 57549. On écrit alors le chiffre 2 à droite du chiffre 9 déjà trouvé.
On effectue la soustraction 57549 - 49688, le résultat est placé à gauche.


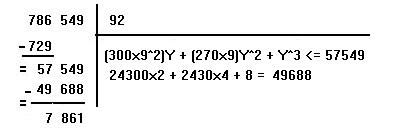
On peut dire que la racine cubique de 786549 est 92 à l'unité près. Si l'on souhaite calculer les décimales après la virgule, on descend une tranche de 3 zéros à droite du résultat de la soustraction et l'on reprend le procédé. On voit que l'on doit rapidement manipuler des nombres de plus en plus grands. Il faut donc envisager pour un tel calcul une programmation en multiprécision. C'est ce que vous trouverez bientôt sur la page principale du site.


___________________________________________________________

III. EXTRACTION DES RACINES QUATRIEMES


La technique étant similaire, je serai plus bref : On découpe le nombre en tranches de 4 chiffres à partir de la droite. On le dispose comme précédemment.
1) On recherche le chiffre le plus grand qui, élevé à la puissance 4 est inférieur ou égal à la tranche de gauche. On le place à droite de la barre verticale. (On l'appelle A). On l'élève à la puissance 4 et on soustrait ce résultat de la tranche de gauche.
2) On abaisse la tranche suivante. On appelle S le nombre obtenu.
On calcule 3 coefficients (C1, C2, C3) :
C1 = 4000 x (A^3)
C2 = 600 x (A^2)
C1 = 40 x A
On injecte ces 3 coefficients dans l'inéquation en Y du quatrième degré suivante :
[C1.Y ] + [C2.(Y^2)] + [C3.(Y^3)] + (Y^4) <= S
On recherche le plus grand Y qui vérifie cette inéquation. Lorsqu'il est trouvé, on le place à droite de A.
A devient donc égal à l'ancien A multiplié par 10 auquel on ajoute Y. On effectue la soustraction avec S du résultat de l'inéquation. On retourne alors en 2). Lorsqu'il n'y a plus de tranches, on abaisse une tranche de 4 zéros, et on met une virgule à droite de A.


___________________________________________________________

IV. EXTRACTION DES RACINES CINQUIEMES


La technique étant similaire, je serai encore plus bref : On découpe le nombre en tranches de 5 chiffres à partir de la droite. On le dispose comme précédemment.
1) On recherche le chiffre le plus grand qui, élevé à la puissance 5 est inférieur ou égal à la tranche de gauche. On le place à droite de la barre verticale. (On l'appelle A). On l'élève à la puissance 4 et on soustrait ce résultat de la tranche de gauche.
2) On abaisse la tranche suivante. On appelle S le nombre obtenu.
On calcule 4 coefficients (C1, C2, C3,C4) :
C1 = 50000 x (A^4)
C2 = 10000 x (A^3)
C3 = 1000 x (A^2)
C4 = 50 x A
On injecte ces 4 coefficients dans l'inéquation en Y du cinquième degré suivante :
[C1.Y ] + [C2.(Y^2)] + [C3.(Y^3)] + [C4.(Y^4)] + (Y^5) <= S
On recherche le plus grand Y qui vérifie cette inéquation. Lorsqu'il est trouvé, on le place à droite de A. On effectue la soustraction avec S du résultat de l'inéquation. On retourne alors en 2). Lorsqu'il n'y a plus de tranches, on abaisse une tranche de 5 zéros, et on met une virgule à droite de A.

___________________________________________________________

V. GENERALISATION DE L'ALGORITHME A L'ORDRE n


Les observateurs auront déjà constaté qu'il y a une corrélation directe avec la formule du binôme. Voici donc l'explication :
...patience, à venir.